Chemguide: Core Chemistry 14 - 16

The effect of concentration on the rates of chemical reactions

This page explains why changing the concentration changes reaction rates, and illustrates it with the reaction between dilute hydrochloric acid and sodium thiosulfate solution.

Why does increasing the concentration increase rates of reaction?

Particles can only react if they collide - and they not only have to collide, but must collide with enough energy for something to happen, and may need to collide the right way round if the particle is a more complicated shape than a single atom or ion.

Increasing the concentration simply means that the particles are going to hit each other more often.

Illustrating this experimentally

A simple quick experiment

Take the reaction between marble chips and dilute hydrochloric acid, for example.

CaCO₃(s) + 2HCl(aq)   CaCl₂(aq) + CO₂(g) + H₂O(l)

If you do this with small marble chips and ordinary bench dilute hydrochloric acid, you get a good supply of bubbles of carbon dioxide produced.

If you dilute the hydrochloric acid by a factor of 10, the reaction is much less vigorous and the flow of carbon dioxide is much slower.

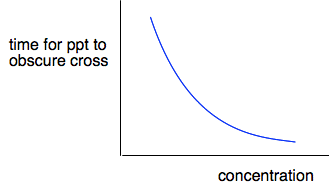
A more detailed experiment

A commonly used experiment to show the effect of concentration on rate is between dilute hydrochloric acid and sodium thiosulfate solution.

Na₂S₂O₃(aq) + 2HCl(aq)  2NaCl(aq) + SO₂(g) + S(s) + H₂O(l)

At this stage, the only place you are likely to come across sodium thiosulfate is in this reaction.

The interesting thing about the reaction is the formation of a precipitate of sulfur. This is formed slowly and appears first as a very pale cream solid which turns yellow as more of it is formed.

In the video you are going to watch, the time taken to form a very small fixed amount of sulfur is measured at various concentrations of sodium thiosulfate, keeping everything else the same.

As you will see, the more dilute the sodium thiosulfate, the longer the time it takes for that amount of sulfur to form.

At one point, the presenter talks about the "dependent variable" and the "independent variable", and I need to be sure that you understand the terms because you will meet them again later.

The dependent variable is the one that changes as a result of something you are doing. In this case, the dependent variable is the time taken for the cross to disappear, because that is changing as a result of you changing the concentration.

The independent variable is the one that you are changing - in this case, the concentration.

The independent variable is always plotted on the x-axis, and the dependent one on the y-axis. The video showed a graph of the results of time taken against concentration and looked like this.

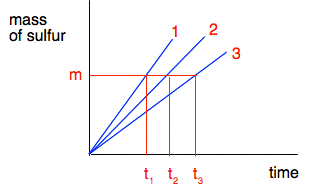
As it stands, this isn't actually very helpful. All it shows is that as you increase the concentration, the time taken for the cross to disappear gets less. But you can see that just by looking at it.

It would be much better if we could find a more precise relationship between the rate of the reaction and the concentration.

If you have read the page about the effect of surface area on rates of reaction, you will have read about "initial rate" experiments. This is another initial rate experiment.

You are finding the time taken for a very small amount of sulfur to be produced at the very beginning of the reaction as you vary concentration.

If you could do a complete plot of the mass of sulfur being formed against time, you would get a curve starting steeply, slowing down, and then stopping - exactly like the one you saw on the previous page.

But at the very beginning of the reaction, the curve is almost a straight line. So if you consider plots of the very early parts of three reactions to produce a fixed mass of sulfur in this experiment, the graphs would look like this.

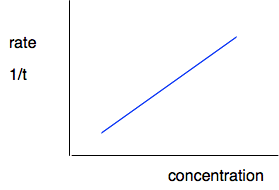
The initial rates would be m/t₁, m/t₂ and m/t₃ grams of sulfur per second.

You don't know what m is of course - that would depend, amongst other things, on how thick your cross was, and how good your eyesight is. But it is always going to be the same in every experiment.

What you can say is that the initial rate is proportional to 1/t - or inversely proportional to t, if you prefer.

If it takes half as long for the cross to disappear, the rate is twice as fast; if it takes 4 times as long for the cross to disappear, the rate is only a quarter as fast.

On a graph, we can use this by plotting 1/t as a measure of rate. It isn't an actual rate, but it allows you to compare rates.

Doing this shows that in this reaction, you have a straight line relationship between concentration and rate - rate is proportional to concentration.