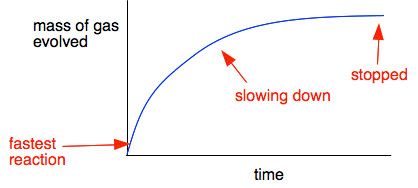
Chemguide: Core Chemistry 14 - 16

The effect of surface area on the rates of chemical reactions

This page uses the reaction between marble chips and dilute hydrochloric acid to investigate the relationship between the rate of reaction and the surface area of the marble chips.

It uses a video which lets you see a commonly done experiment as it happens in the lab, and allows you to record and process your own results if you want to.

The reaction between marble chips and dilute hydrochloric acid

Marble is a pure form of calcium carbonate. As with all carbonates, it reacts with acids to produce a salt, carbon dioxide and water.

CaCO₃(s) + 2HCl(aq)   CaCl₂(aq) + CO₂(g) + H₂O(l)

The important part of the acid is the presence of hydrogen ions. These react with carbonate ions in the solid calcium carbonate.

CO₃^2-(s) + 2H⁺(aq)   CO₂(g) + H₂O(l)

The importance of collisions between particles in reactions

Hydrogen ions and carbonate ions can only react if they come into contact with each other. Because calcium carbonate is a solid, any reaction can only take place on the surface of the solid.

If you had a large marble chip, all the calcium carbonate in the middle of the chip can't react with the acid, because the acid can't get at it.

But if you had the same mass of smaller chips, you have opened up a much larger surface area for the acid to attack.

So you might expect that the smaller the marble chips were, the faster the reaction would be.

The experiment

The video shows three separate experiments using the same mass of marble and the same volume of the same hydrochloric acid to explore the rate of the reaction between the acid and three different sized marble chips.

It measure the mass of carbon dioxide being given off as each reaction proceeds.

The video is quite long (about 16 minutes) and gives you the opportunity to record results as if the experiment was in front of you in the lab.

It doesn't seem a good use of your time to watch this from start to finish, but it would be worth watching the whole of the first reaction (about 6 minutes) and the beginning of the second one, and recording those results.

In case you missed it, the point of the cotton wool is to stop spray from the reaction escaping from the flask and altering the mass lost.

The results

I'm not going to use the figures from the experiment because it isn't easy to convert those into a decent graph for web purposes. So I am going to generalise them.

Just looking at one reaction

You will get a graph of this form.

The rate of the reaction at any one time is given by the slope of the graph.

• If the slope is steep, it means that a lot of carbon dioxide is being given off at that time. The reaction is fast.

• When the slope is shallower, it means that less carbon dioxide is being given off at that time. The reaction is slowing down.

• Where the graph becomes horizontal, there is no increase at all in the mass of carbon dioxide being produced. The reaction has stopped.

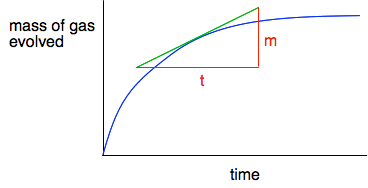
Measuring the rate of the reaction at any point

You just need to measure how steep the curve is at whatever time you happen to be interested in.

To do this, you draw a tangent to the curve at that point, and then a triangle so that you can measure the mass, m, generated in a time, t.

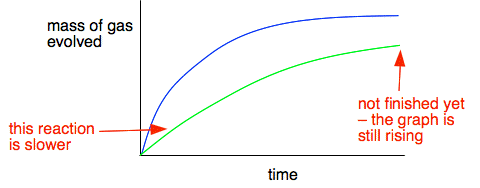
The slope of the curve at that point is then m/t - and that gives you the rate of reaction at that point in grams of carbon dioxide being produced per second.

Adding another reaction

Suppose that the graph is for fairly small marble chips. If you compared this with the graph for larger marble chips, what differences and similarities would you expect?

You would expect the reaction to be slower because the surface area of the larger chips is less. So the graph would be less steep at the beginning.

But eventually, if you waited long enough, you would get the same mass loss if you started with the same mass of marble and the same volume of the same hydrochloric acid.

The total amount of reaction is dependent on the acid because there is a large excess of marble. At the end of the experiment, you will hardly notice any change in the amount of marble present.

So if you have the same amount of acid, you will eventually get the same mass of carbon dioxide produced.

On the next graph, the green line represents results from larger marble chips.

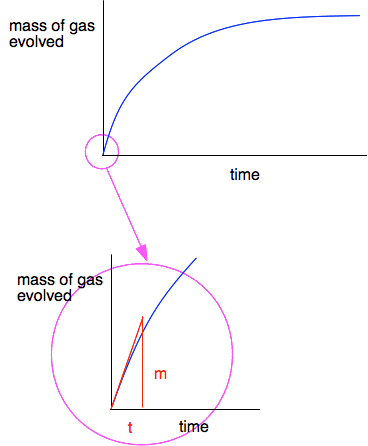
The usefulness of the initial rate

If you watched the video to the end, you will know that the presenter asked you to draw tangents to each graph at the beginning of the reaction to measure the initial rate of each reaction.

Let's show that on the initial blue curve.

The initial curve is almost, but not quite, a straight line. So you draw your best guess at a tangent from the zero point, and then measure the initial rate as m/t - measured in grams of CO₂ per second.

Finding the initial rate is a common way of comparing the rates of a reaction as you change one of the variables in the reaction - the state of division of a solid, the concentration of a liquid, the temperature, and so on.

At the very start of the reaction, you know everything essential about the reaction. You know all the concentrations (and masses if you have got a solid involved), and you know the temperature. It is the only point at which you know everything exactly without having to work it out.

You will come across another initial rate experiment in the next page in this sequence - that time concerning concentrations.

Another way of comparing the initial rates of this reaction

You could also do this by timing how long it took to produce a small amount of carbon dioxide as you varied the sizes of the marble chips. This time you would get initial rates measured in cm³ of gas per second.

You know how vigorously magnesium burns in air. If you use magnesium powder, and sprinkle it into a flame, it does burn very vigorously. But if you heat a pile of magnesium powder on a piece of ceramic paper on a tripod and gauze, it is quite disappointing.

What has happened is that the powder is so fine (and can't move) that hardly any air can get between the particles of magnesium. Its surface area exposed to the air is basically just the top surface of the pile.