THE EFFECT OF CATALYSTS ON REACTION RATES

This page describes and explains the way that adding a catalyst affects the rate of a reaction. It assumes that you are already familiar with basic ideas about the collision theory of reaction rates, and with the Maxwell-Boltzmann distribution of molecular energies in a gas.

Note that this is only a preliminary look at catalysis as far as it affects rates of reaction. If you are looking for more detail, there is a separate section dealing with catalysts which you can access via a link at the bottom of the page.

The facts

What are catalysts?

A catalyst is a substance which speeds up a reaction, but is chemically unchanged at the end of the reaction. When the reaction has finished, you would have exactly the same mass of catalyst as you had at the beginning.

Some examples

Some common examples which you may need for other parts of your syllabus include:

The explanation

The key importance of activation energy

Collisions only result in a reaction if the particles collide with a certain minimum energy called the activation energy for the reaction.

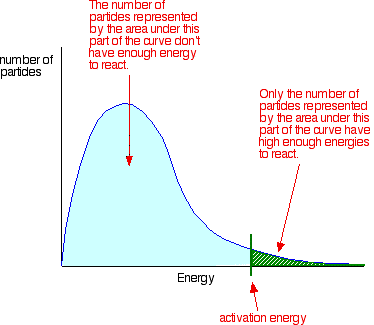
You can mark the position of activation energy on a Maxwell-Boltzmann distribution to get a diagram like this:

Only those particles represented by the area to the right of the activation energy will react when they collide. The great majority don't have enough energy, and will simply bounce apart. If there are very few particles with enough energy at any time, then the reaction will be slow.

So a low energy particle could, an instant later, have gained enough energy from a collision that it could now react. And the opposite is true. A more energetic particle which didn't happen to collide successfully and produce a reaction, could find itself slowed down an instant later as a result of a collision.

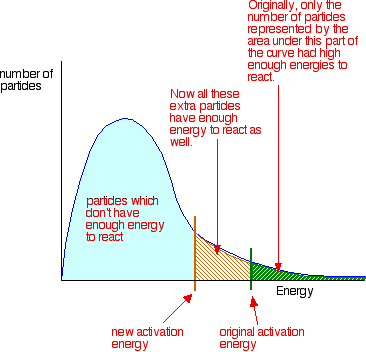
Catalysts and activation energy

To increase the rate of a reaction you need to increase the number of successful collisions. One possible way of doing this is to provide an alternative way for the reaction to happen which has a lower activation energy.

In other words, to move the activation energy on the graph like this:

As before, particles which don't have enough energy at a particular time will at some time in the future gain energy from random collisions, just as other particles will lose energy. You mustn't get the idea that those particles in the blue area of the graph can never react - given time they will.

Adding a catalyst has exactly this effect of shifting the activation energy. A catalyst provides an alternative route for the reaction. That alternative route has a lower activation energy. Showing this on an energy profile:

A word of caution!

Be very careful if you are asked about this in an exam. The correct form of words is

"A catalyst provides an alternative route for the reaction with a lower activation energy."

It does not "lower the activation energy of the reaction". There is a subtle difference between the two statements that is easily illustrated with a simple analogy.

Suppose you have a mountain between two valleys so that the only way for people to get from one valley to the other is over the mountain. Only the most active people will manage to get from one valley to the other.

Now suppose a tunnel is cut through the mountain. Many more people will now manage to get from one valley to the other by this easier route. You could say that the tunnel route has a lower activation energy than going over the mountain.

But you haven't lowered the mountain! The tunnel has provided an alternative route but hasn't lowered the original one. The original mountain is still there, and some people will still choose to climb it.

In the chemistry case, if particles collide with enough energy they can still react in exactly the same way as if the catalyst wasn't there. It is simply that the majority of particles will react via the easier catalysed route.