Chemguide: Core Chemistry 14 - 16

Measuring enthalpy change practically

This page introduces the term "enthalpy change" and looks at how it can be measured using simple lab experiments.

You need to check your syllabus and past papers to find out how much of this you need to know.

Enthalpy change

I am assuming that you already know about endothermic and exothermic reactions. If not, explore the energy menu before you go on.

Enthalpy change is simply a measure of the amount of heat evolved or absorbed during a reaction.

It is no more difficult than that!

It is given the symbol ΔH - read as "delta H".

The enthalpy change is always based on the reactants.

If a reaction gives out heat, the reactants must have lost that amount of energy, and so ΔH is given a negative value, such as -100 kJ mol^-1 (read as "kilojoules per mole").

If a reaction absorbs heat, then the reactants must have gained heat and so ΔH is given a positive value, such as +50 kJ mol^-1.

So . . .

An exothermic reaction has a negative value for ΔH.

An endothermic reaction has a positive value for ΔH.

It is essential that you get those the right way round.

Measuring enthalpy changes

Enthalpy changes are found by measuring the temperature change produced by the reaction.

If the reaction includes a liquid, you can measure the temperature change of the liquid.

If you are finding the enthalpy change of combustion, you can use the heat produced to warm up some water, and measure the temperature increase in that.

A bit of physics

Specific heat capacity

In the olden days, a calorie was defined as the amount of heat necessary to raise the temperature of 1 g of water by 1 °C. That is called the specific heat capacity of water.

Nowadays, the joule has replaced the calorie as the unit of heat, and 1 calorie is equivalent to 4.18 joules. So the specific heat capacity of water is now

4.18 J g^-1 °C^-1

You read that as "4.18 joules per gram per degree Celcius".

In every case, the specific heat capacity of any substance is the number of joules needed to raise the temperature of 1 g of it by 1 °C.

So you can work out the amount of heat produced by a reaction using

heat produced = mass (g) x specific heat capacity x temperature change (ΔT)

Also written as:

Q = m c ΔT

The symbol Δ (delta) means "change in".

If you had an endothermic change, then you would have to rephrase that as

heat absorbed = mass (g) x specific heat capacity x temperature change (ΔT)

Measuring the enthalpy change of combustion of ethanol

The video shows a simple method for doing this in a school lab.

The interesting bit about this video is the discussion of the errors involved. The presenter says at the end ". . . the enthalpy of combustion you will see is rather lower than data book values".

That will turn out to be an understatement!

Let's take the experimental results from this video and calculate the enthalpy change of combustion of ethanol.

Mass of water in calorimeter = 120 g

Mass of burner + ethanol before = 192.34 g

Mass of burner + ethanol after = 191.92 g

Mass of ethanol burned = 0.42 g

Temperature originally = 26 °C

Temperature after = 34 °C

Temperature rise = 8°C

The first thing to do is to calculate the amount of heat given off using the formula above.

We make the assumption that the only thing being heated is the water in the calorimeter. That of course, is nonsense! We are also heating the copper calorimeter, the gauze, the metal support, the stirrer, the thermometer, and the air - and this is the major source of error. And, of course, you have to add on other errors like incomplete combustion and insufficiently accurate thermometers.

heat evolved = m c ΔT = 120 x 4.18 x 8 J = 4000 J

I am only quoting this to 2 significant figures. Even that is a greater accuracy than the experiment deserves!

Enthalpy changes are always quoted in kilojoules, so we first need to divide this value by 1000.

heat evolved = 4000/1000 = 4.0 kJ

That was given out when 0.42 g of ethanol were burned. How much would be evolved when 1 mole is burned? (RAMs: H = 1; C = 12; O = 16)

1 mol C₂H₅OH weighs (2 x 12) + (6 x 1) + 16 = 46 g

0.42 g ethanol gave 4.0 kJ

46 g ethanol would give 4.0 x 46/0.42 = 440 kJ

The enthalpy change of combustion of ethanol is therefore -440 kJ mol^-1.

(The negative sign showing that the reaction is exothermic.)

And the data book value? -1371 kJ mol^-1.

This is a spectacularly bad result - but it doesn't matter in this context.

We have seen how the experiment might be done, and looked at the major errors involved which suggest that this isn't a realistic way of getting an accurate result. And we have shown how you can process the results.

Accurate results need access to equipment which you won't normally find in a school lab.

Measuring the enthalpy change of the reaction between copper(II) sulfate solution and zinc

CuSO₄(aq) + Zn(s)     ZnSO₄(aq) + Cu(s)

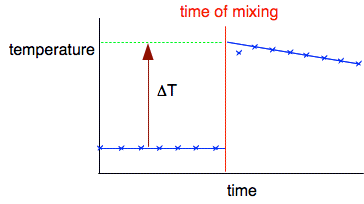
You can get much better results in reactions like this which can be done in a polystyrene cup. The polystyrene is a good insulator and has a very low mass, so hardly any heat will be used in warming that up.

The next video is quite long. You will have to ignore the unconventional spelling!

I suggest you pause the video at 5:26 and ignore the rest of it which deals with the calculation. That is better done written down - as below.

I need to discuss the purpose of the graph, so keep that on the screen before you read on.

The reason for the graph

The temperature rise is quite large (48°C), and at that temperature heat will be being lost - for example, through the uninsulated lid.

You can see the effect of that heat loss by the fact that the graph starts to fall when the reaction is over.

You can compensate for the heat loss by extrapolating the cooling part of the graph back to the time of mixing to give a better estimate of what the maximum temperature would be in the absence of any heat loss.

You plot enough points before mixing in order to be sure that the liquid is at constant room temperature.

Then you get a quick rise in temperature as the reaction happens before it starts to cool again.

Once you have established that the cooling is happening at a steady rate, you extrapolate the cooling curve back to the point of mixing to give a reasonable estimate of the temperature rise you would have got if there was no cooling.

It is then an easy job to measure the overall temperature rise, ΔT.

Results

Volume of 1 mol dm^-3 CuSO₄ = 25 cm³

Mass of zinc (a large excess) = 6 g

Temperature rise from graph = 48.0°C

Calculation

Assuming the density of the CuSO₄ solution is the same as water,
mass of CuSO₄ solution = 25 g

Assuming the specific heat capacity of copper(II) sulfate solution is the same as water,
heat evolved by reaction = m c ΔT = 25 x 4.18 x 48 = 5016 J

Enthalpy changes are always measured in kJ, so we need to divide by 1000: 5.016 kJ

1000 cm³ of 1 mol dm^-3 CuSO₄ contains 1 mol.

25 cm³ of 1 mol dm^-3 CuSO₄ contains 25/1000 x 1 = 0.025 mol.

Heat evolved if 1 mol CuSO₄ reacted = 5.016/0.025 = 200 kJ

Enthalpy change of reaction is -200 kJ mol^-1.

Comments

If you watched the video to the end, you were told that the accepted value for this enthalpy change was -219 kJ mol^-1. So this result is in the right area, but is still about 10% adrift.

There are several problems with this calculation.

• You have a sizeable amount of metal present in the cup - first, the excess zinc and then the copper which is formed during the reaction. They are gaining heat as well, but we aren't taking that into account.

• We are assuming the density of the copper(II) sulfate solution is the same as water. I found one figure for the density of 1 mol dm^-3 CuSO₄ of 1.2 g cm^-3. If you use that value instead of the density of water you will get an answer 20% bigger!

• I haven't been able to find a value for the specific heat capacity of the copper(II) sulfate solution, but I suspect that it isn't exactly the same as that of water.

Don't worry about this unless you have to account for a value found from your own experiment. If you are asked something like this in an exam, the numbers will probably be made up anyway to give a reasonable answer.