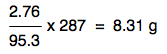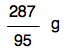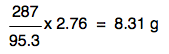|
Chemguide: Core Chemistry 14 - 16 Calculations from equations involving masses This page shows how you can use moles to calculate useful things involving masses from the equation for a reaction. I am assuming you have already read and understood the page about moles. There are two different approaches to this, each with its own advantages and disadvantages. I am going to start with the one that I have used throughout my teaching career. Students starting doing chemistry calculations often dislike moles. This method gets rid of them very early on in the sum so that you can work in more familiar units. But it is also essential that you can see the logic of the second method, because you will need that same logic when you come to doing titration calculations in a later page. Sample calculations Example 1 Calcium carbonate and dilute hydrochloric acid react together according to this equation:
What mass of carbon dioxide would you get if you added excess hydrochloric acid to 10 g of calcium carbonate? (RAMs: C = 12; O = 16; Ca = 40) Start by writing down what the equation says in terms of moles. Remember that you can read each formula as an amount in moles. So for example, CaCO3 + 2HCl can be read as 1 mole of CaCO3 plus 2 moles of HCl. So the equation says that
You aren't interested in anything else. The hydrochloric acid is in excess, and you aren't asked about the calcium chloride. Now convert the amounts in moles into grams
So the equation is saying that:
And that's the chemistry finished with - it just involves a simple sum now. How much carbon dioxide would you get if you only started with 10 g? That's trivial! You started with a tenth as much calcium carbonate, and so will get a tenth as much CO2: 4.4 g. I have deliberately chosen this example to start with using easy numbers. All that will differ in the rest of the examples is this little calculation on the end. The chemistry is over once you have converted the equation quantities into masses. I have used lots of words in this, but your final calculation would look like this:
You must show all your working. In an exam, if you make a silly mistake, your examiner has to be able to trace where that mistake is in order to give you credit for everything else. Example 2 Let's make the numbers a bit more awkward! Suppose you had a solution of magnesium chloride made by dissolving 2.76 g of anhydrous magnesium chloride, MgCl2, in water, and then added an excess of silver nitrate solution to it to give a white precipitate of silver chloride. What mass of silver chloride would be formed?
(RAMs: Mg = 24.3; Cl = 35.5; Ag = 108) Start by interpreting the equation in terms of moles, only concentrating on the things you are interested in.
Convert these into grams.
So the equation is saying that:
All that is left to do is to work out how much 2.76 g of MgCl2 would give. This is just a simple proportion sum, and if you are happy with those, you will spot that the answer would be
But suppose you don't immediately see that? You can just put in an extra step. Work out how much 1 gram of MgCl2 would produce by dividing 287 by 95. 1 gram of MgCl2 would produce:
. . . and so 2.76 g would produce:
That's exactly the same expression as before with the numbers rearranged slightly. It doesn't matter how you do this - all that matters is that you get the right answer. Notice that the answer is only quoted to 3 significant figures. That's because your original mass of MgCl2 was only quoted to 3 significant figures. The final calculation would look like this:
. . . or insert another step involving 1 gram if you feel more comfortable doing that. Example 3 If you do the calculations this way, it makes it very easy to work in units other than grams, and without worrying about conversion factors. Here is an example. Titanium is manufactured by heating titanium(IV) chloride with sodium.
What mass of sodium would be required to produce 1 tonne of titanium? (RAMs: Na = 23; Ti = 48)
But you aren't being asked about the amount of Ti in grams! You could work out how many grams there are in a tonne, but it is totally unnecessary. Whatever mass unit you are using, the ratio between the sodium and the titanium will always be the same. The units may vary, but the ratio is always going to be 92 Na : 48 Ti. It could be:
. . . and any other mass unit that you might come across. So:
This would be a lot more tedious using the alternative version of the calculation which is coming up next. Up to now I have been using the complete word "mole". In calculations the abbreviation "mol" is commonly used, and I shall use that from now on. Example 4 It is quite likely that you will come across another route through this sort of calculation forced on you by an examiner in a question on a structured paper. You may, of course, just be asked to do the calculation with a single blank space to do it in - in which case you can do it however you want to. But the examiner could also split the calculation up into stages to help you through it. Suppose you had a solution of potassium iodide in water containing 4.98 g of KI, and then added an excess of lead(II) nitrate solution to it to give a yellow precipitate of lead(II) iodide.
(a) Calculate the number of moles of potassium iodide used. (b) Calculate the number of moles of lead(II) iodide formed. (c) Calculate the mass of lead(II) iodide formed. (RAMs: K = 39; I = 127; Pb = 207)
Quote your answers to 3 significant figures because that is the accuracy of the mass you started with. Example 5 This example uses the same route through the calculation as the last one, but without the guidance. Calculate the mass of potassium nitrate you would have to heat to produce 1.60 g of oxygen.
(RAMs: N = 14; O = 16; K = 39) There is a standard route map for calculations like these:
The calculation looks like this:
Percentage yields We'll look at another example of the sort of sum we've just been doing and calculate what mass of magnesium chloride crystals you would get if you treated 2.43 g of magnesium with a slight excess of dilute hydrochloric acid. There are two equations - one for the actual reaction, and one for the crystallisation.
(RAMs: H=1; O = 16; Mg = 24.3; Cl = 35.5) The calculation goes like this - starting with what you know most about, the magnesium.
There is nothing new in this! But suppose you actually did this experiment using 2.43 g of magnesium, and weighed the crystals you produced, and found that you had actually made only 19.5 g. Your percentage yield would be 19.5/20.33 x 100 = 95.9%. Where did the rest go? Perhaps you didn't crystallise all the solution. Perhaps you evaporated it a bit vigorously and droplets spat out of the evaporating basin. Perhaps you evaporated it so vigorously that some of the crystals lost their water of crystallisation. There are all sorts of reasons why a percentage yield may be less than 100%. Finally The only way to get good at doing chemistry calculations is by doing lots of them, and the best source is past papers for whatever exam you are preparing for, together with the accompanying mark schemes. You will find links to the main UK Exam Boards on this page. Some Exam Boards are far more generous with their past papers than others. There is no reason why you couldn't look at papers from other examiners, but bear in mind that their syllabuses might be different. On the other hand, chemistry calculations are much the same whatever the rest of the syllabus might contain.
© Jim Clark 2021 |