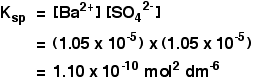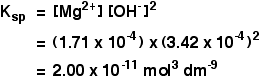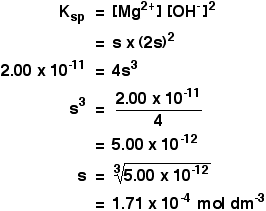|
SOLUBILITY PRODUCT CALCULATIONS This page is a brief introduction to solubility product calculations. These are covered in more detail in my chemistry calculations book. Calculating solubility products from solubilities I am going to assume that you are given the solubility of an ionic compound in mol dm-3. If it was in g dm-3, or any other concentration units, you would first have to convert it into mol dm-3. Example 1 The solubility of barium sulphate at 298 K is 1.05 x 10-5 mol dm-3. Calculate the solubility product. The equilibrium is:
Notice that each mole of barium sulphate dissolves to give 1 mole of barium ions and 1 mole of sulphate ions in solution. That means that:
All you need to do now is to put these values into the solubility product expression, and do the simple sum.
Don't forget to work the units out. | ||
|
Important: Get your calculator and work this out! Students frequently mis-enter numbers like 1.05 x 10-5. If you try this sum, and get a different answer, then you are probably misusing the EXP button. To enter this number, you would enter 1.05, press the EXP button, and then enter -5 (probably by entering 5 and then pressing the +/- button). People often try to enter x 10 in the middle of this process as well. The EXP button includes this. | ||
|
Example 2 These calculations are very simple if you have a compound in which the numbers of positive and negative ions are 1 : 1. This next example shows you how to cope if the ratio is different. The solubility of magnesium hydroxide at 298 K is 1.71 x 10-4 mol dm-3. Calculate the solubility product. The equilibrium is:
For every mole of magnesium hydroxide that dissolves, you will get one mole of magnesium ions, but twice that number of hydroxide ions. So the concentration of the dissolved magnesium ions is the same as the dissolved magnesium hydroxide:
The concentration of dissolved hydroxide ions is twice that:
Now put these numbers into the solubility product expression and do the sum.
Calculating solubilities from solubility products Reversing the sums we have been doing isn't difficult as long as you know how to start. We will take the magnesium hydroxide example as above, but this time start from the solubility product and work back to the solubility. If the solubility product of magnesium hydroxide is 2.00 x 10-11 mol3 dm-9 at 298 K, calculate its solubility in mol dm-3 at that temperature.
The trick this time is to give the unknown solubility a symbol like x or s. I'm going to choose s, because an x looks too much like a multiplication sign. If the concentration of dissolved magnesium hydroxide is s mol dm-3, then:
Put these values into the solubility product expression, and do the sum.
| ||
|
Note: This is where you might need to find your calculator instruction book! With a bit of luck, you will find a button for cube roots, and this will enable you to do sums with compounds like magnesium hydroxide with a formula AB2 or A2B. Anything more complicated than this would need you to be able to find 4th or 5th roots. It would be a good idea to find out how your calculator does this. Mine has an x1/y button. You would need to practice using this or something similar. On my calculator, to find fourth root of 16 using this button, you would have the number 16 in the display, press the x1/y button, enter 4 (for 4th root) and then press equals. If you have done it right, you should get an answer of 2. | ||
To the solubility product menu . . . © Jim Clark 2011 (modified November 2013) |
||