|
THERMAL STABILITY OF THE GROUP 2 CARBONATES AND NITRATES This page looks at the effect of heat on the carbonates and nitrates of the Group 2 elements - beryllium, magnesium, calcium, strontium and barium. It describes and explains how the thermal stability of the compounds changes as you go down the Group. The Facts The effect of heat on the Group 2 carbonates All the carbonates in this Group undergo thermal decomposition to give the metal oxide and carbon dioxide gas. Thermal decomposition is the term given to splitting up a compound by heating it. All of these carbonates are white solids, and the oxides that are produced are also white solids. If "X" represents any one of the elements:
As you go down the Group, the carbonates have to be heated more strongly before they will decompose.
The effect of heat on the Group 2 nitrates All the nitrates in this Group undergo thermal decomposition to give the metal oxide, nitrogen dioxide and oxygen. The nitrates are white solids, and the oxides produced are also white solids. Brown nitrogen dioxide gas is given off together with oxygen. Magnesium and calcium nitrates normally have water of crystallisation, and the solid may dissolve in its own water of crystallisation to make a colourless solution before it starts to decompose. Again, if "X" represents any one of the elements:
As you go down the Group, the nitrates also have to be heated more strongly before they will decompose.
Summary Both carbonates and nitrates become more thermally stable as you go down the Group. The ones lower down have to be heated more strongly than those at the top before they will decompose. Explanations This page offers two different ways of looking at the problem. You need to find out which of these your examiners are likely to expect from you so that you don't get involved in more difficult things than you actually need. You should look at your syllabus, and past exam papers - together with their mark schemes | ||||||||||||
|
Note: If you are working towards a UK-based exam (A level or its equivalent) and haven't got copies of your syllabus and past papers follow this link to find out how to get hold of them. | ||||||||||||
|
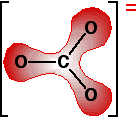
Detailed explanations are given for the carbonates because the diagrams are easier to draw, and their equations are also easier. Exactly the same arguments apply to the nitrates. Explaining the trend in terms of the polarising ability of the positive ion A small 2+ ion has a lot of charge packed into a small volume of space. It has a high charge density and will have a marked distorting effect on any negative ions which happen to be near it. A bigger 2+ ion has the same charge spread over a larger volume of space. Its charge density will be lower, and it will cause less distortion to nearby negative ions. The structure of the carbonate ion If you worked out the structure of a carbonate ion using "dots-and-crosses" or some similar method, you would probably come up with:
This shows two single carbon-oxygen bonds and one double one, with two of the oxygens each carrying a negative charge. Unfortunately, in real carbonate ions all the bonds are identical, and the charges are spread out over the whole ion - although concentrated on the oxygen atoms. We say that the charges are delocalised. This is a rather more complicated version of the bonding you might have come across in benzene or in ions like ethanoate. For the purposes of this topic, you don't need to understand how this bonding has come about. | ||||||||||||
|
Note: If you are interested, you could follow these links to benzene or to organic acids. Either of these links is likely to involve you in a fairly time-consuming detour! | ||||||||||||
|
The next diagram shows the delocalised electrons. The shading is intended to show that there is a greater chance of finding them around the oxygen atoms than near the carbon.
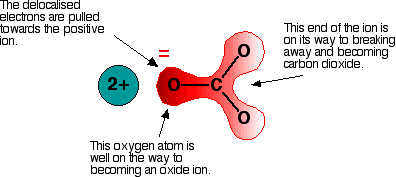
Polarising the carbonate ion Now imagine what happens when this ion is placed next to a positive ion. The positive ion attracts the delocalised electrons in the carbonate ion towards itself. The carbonate ion becomes polarised.
If this is heated, the carbon dioxide breaks free to leave the metal oxide. How much you need to heat the carbonate before that happens depends on how polarised the ion was. If it is highly polarised, you need less heat than if it is only slightly polarised. The smaller the positive ion is, the higher the charge density, and the greater effect it will have on the carbonate ion. As the positive ions get bigger as you go down the Group, they have less effect on the carbonate ions near them. To compensate for that, you have to heat the compound more in order to persuade the carbon dioxide to break free and leave the metal oxide. In other words, as you go down the Group, the carbonates become more thermally stable. What about the nitrates? The argument is exactly the same here. The small positive ions at the top of the Group polarise the nitrate ions more than the larger positive ions at the bottom. Drawing diagrams to show this happening is much more difficult because the process has interactions involving more than one nitrate ion. You wouldn't be expected to attempt to draw this in an exam. Explaining the trend in terms of the energetics of the process Looking at the enthalpy changes If you calculate the enthalpy changes for the decomposition of the various carbonates, you find that all the changes are quite strongly endothermic. That implies that the reactions are likely to have to be heated constantly to make them happen. | ||||||||||||
|
Note: If you aren't happy about enthalpy changes, you might want to explore the energetics section of Chemguide, or my chemistry calculations book. | ||||||||||||
|
The enthalpy changes (in kJ mol-1) which I calculated from enthalpy changes of formation are given in the table. Figures to calculate the beryllium carbonate value weren't available. Remember that the reaction we are talking about is:
You can see that the reactions become more endothermic as you go down the Group. That's entirely what you would expect as the carbonates become more thermally stable. You have to supply increasing amounts of heat energy to make them decompose. Explaining the enthalpy changes Here's where things start to get difficult! If you aren't familiar with Hess's Law cycles (or with Born-Haber cycles) and with lattice enthalpies (lattice energies), you aren't going to understand the next bit. Don't waste your time looking at it. Using an enthalpy cycle You can dig around to find the underlying causes of the increasingly endothermic changes as you go down the Group by drawing an enthalpy cycle involving the lattice enthalpies of the metal carbonates and the metal oxides. Confusingly, there are two ways of defining lattice enthalpy. In order to make the argument mathematically simpler, during the rest of this page I am going to use the less common version (as far as UK A level syllabuses are concerned): Lattice enthalpy is the heat needed to split one mole of crystal in its standard state into its separate gaseous ions. For example, for magnesium oxide, it is the heat needed to carry out 1 mole of this change: MgO(s) | ||||||||||||
|
Note: Lattice enthalpy is more usually defined as the heat evolved when 1 mole of crystal is formed from its gaseous ions. In that case, the lattice enthalpy for magnesium oxide would be -3889 kJ mol-1. The term we are using here should more accurately be called the "lattice dissociation enthalpy". | ||||||||||||
|
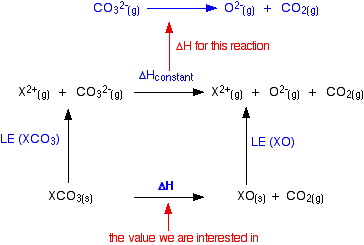
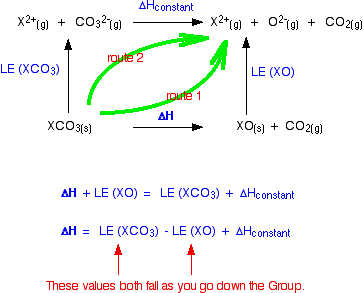
The cycle we are interested in looks like this:
You can apply Hess's Law to this, and find two routes which will have an equal enthalpy change because they start and end in the same places.
For reasons we will look at shortly, the lattice enthalpies of both the oxides and carbonates fall as you go down the Group. But they don't fall at the same rate. The oxide lattice enthalpy falls faster than the carbonate one. If you think carefully about what happens to the value of the overall enthalpy change of the decomposition reaction, you will see that it gradually becomes more positive as you go down the Group.
Explaining the relative falls in lattice enthalpy The size of the lattice enthalpy is governed by several factors, one of which is the distance between the centres of the positive and negative ions in the lattice. Forces of attraction are greatest if the distances between the ions are small. If the attractions are large, then a lot of energy will have to be used to separate the ions - the lattice enthalpy will be large. The lattice enthalpies of both carbonates and oxides fall as you go down the Group because the positive ions are getting bigger. The inter-ionic distances are increasing and so the attractions become weaker.
The lattice enthalpies fall at different rates because of the different sizes of the two negative ions - oxide and carbonate. The oxide ion is relatively small for a negative ion (0.140 nm), whereas the carbonate ion is large (no figure available).
In the oxides, when you go from magnesium oxide to calcium oxide, for example, the inter-ionic distance increases from 0.205 nm (0.140 + 0.065) to 0.239 nm (0.140 + 0.099) - an increase of about 17%. In the carbonates, the inter-ionic distance is dominated by the much larger carbonate ion. Although the inter-ionic distance will increase by the same amount as you go from magnesium carbonate to calcium carbonate, as a percentage of the total distance the increase will be much less. Some made-up figures show this clearly. I can't find a value for the radius of a carbonate ion, and so can't use real figures. For the sake of argument, suppose that the carbonate ion radius was 0.3 nm. The inter-ionic distances in the two cases we are talking about would increase from 0.365 nm to 0.399 nm - an increase of only about 9%. The rates at which the two lattice energies fall as you go down the Group depends on the percentage change as you go from one compound to the next. On that basis, the oxide lattice enthalpies are bound to fall faster than those of the carbonates. What about the nitrates? The nitrate ion is bigger than an oxide ion, and so its radius tends to dominate the inter-ionic distance. The lattice enthalpy of the oxide will again fall faster than the nitrate. if you constructed a cycle like that further up the page, the same arguments would apply.
© Jim Clark 2002 (last modified December 2021) |
||||||||||||